L’auto riconosce la segnaletica verticale e orizzontale e riporta sul display l’indicazione del segnale stradale. Grazie ad altri sensori (banalmente, rilevando la velocità istantanea del veicolo) è in grado di avvertirci se stiamo superando ad esempio il limite di velocità grazie a un allarme acustico o colorando di rosso lo sfondo del segnale sul nostro display.
Applicazioni di questo tipo si basano su quello che si chiama Deep Learning, campo specifico del machine learning e quindi dell’AI che si basa sull’apprendimento basato su reti neurali. Una rete neurale non è altro che un modello matematico, creato per risolvere specifiche problematiche. Quelle che utilizziamo in questo esempio sono le reti neurali convoluzionali, molto efficaci nell’area del riconoscimento delle immagini (ma anche nel riconoscimento del discorso).
Per far sì che l’addestramento funzioni, occorrono grandi quantità di dati sui quali la rete possa apprendere con sufficiente accuratezza (con percentuali che sfiorano il 100% ma comunque sempre nel range 80-100%). Un dataset spesso contiene centinaia di categorie di segnali stradali, decine di migliaia di istanze di immagini di cui più della metà ad alta risoluzione. Importante è usare dataset con almeno 20 immagini per categoria perché sono necessarie a un appropriato Deep Learning della rete neurale. Nell’immagine sotto, un esempio di rete pienamente connessa (fully connected). Ogni neurone della rete ha dei pesi e al termine della rete stessa, vengono prodotti output.
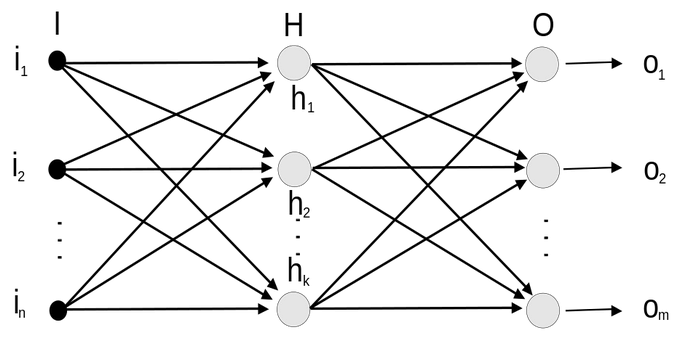
Fonte: https://it.wikipedia.org/wiki/File:Rete-Neurale2.svg
Indice degli argomenti:
Matrici di convoluzione e dataset
La maggioranza dei filtri utilizza matrici di convoluzione. Con il filtro matrice di convoluzione, volendo si può costruire un filtro personalizzato. La convoluzione è il processamento di una matrice attraverso un’altra che viene chiamata kernel.
Scopri i trend AI del 2025: Scarica il report degli Osservatori del Politecnico di Milano
Il filtro matrice di convoluzione utilizza come prima matrice l’immagine da processare. L’immagine è un insieme bidimensionale di pixel in coordinate rettangolari. Il kernel usato dipende dall’effetto che si vuole ottenere.
La progettazione dei kernel si basa su matematica di alto livello. Si possono trovare kernel preconfezionati in rete. Un dato filtro può sfocare la nostra immagine, un altro aumentarne il contrasto, ad esempio. Le matrici kernel sono soprattutto di dimensione dispari, in quanto nella convoluzione è importante identificare il centro della matrice kernel; per esempio possono essere di dimensione 3×3, 5×5 o 7×7. Noi useremo un kernel 3×3.
Il primo passo è sicuramente procurarsi un dataset su cui “addestrare” la nostra rete neurale. Di norma, occorrono tre tipi di dataset:
- di training
- di test
- di validazione
Per la nostra applicazione si tratta di tre semplici file che andremo a caricare in un dizionario interno: una struttura con chiavi/valori che ci servirà per le elaborazioni successive (si tratta di file di non più di 200 MB, disponibili in rete)
Il set di test conterrà cinque immagini scelte fra quelle a disposizione nel dataset. Compito del modello, alla fine della fase di addestramento, sarà riconoscerle con sufficiente accuratezza e quindi bassa probabilità di errore.

Fonte: http://www.vicos.si/Downloads/DFGTSD
Step di pre-processing
Ci sono alcuni passi necessari al trattamento preliminare delle immagini che servono a velocizzare l’elaborazione successiva (addestramento ed elaborazione del modello).
Il primo step propedeutico è la conversione delle immagini in scala di grigio, successivamente avviene la normalizzazione, per poter trattare tutte le immagini in maniera uniforme. Si tratta di una trasformazione lineare che prevede di sottrarre a ogni immagine la media del dataset e dividere il tutto per la deviazione standard. Usare un kernel 3×3 vuol dire che la nostra matrice ha 3 strati, a ogni layer avviene una elaborazione che al termine produce un risultato. L’addestramento di queste reti prevede una codifica modulare che utilizza fra l’altro gradienti stocastici e alcuni ottimizzatori (ottimizzatore di Adam, nello specifico). La profondità di una rete come questa (i livelli del modello) può essere di 16 o 32, nel nostro caso nel codice è stato usato un valore 32 raggiungendo un’accuratezza nel riconoscimento vicina al 94%.
Un’altra tecnica molto utile in questa fase è il dropout. Si tratta di una tecnica di regolarizzazione (brevettata da Google) per ridurre l’overfitting nelle reti neurali. Quando usiamo reti neurali di dimensioni medio-grandi su set di dati relativamente piccoli, possiamo incappare nel sovra-utilizzo dei dati di addestramento, cosa che porta a scarse prestazioni quando il modello viene valutato su nuovi dati. Cosa si fa per evitare questo? Si adattano le possibili reti neurali sullo stesso set di dati e si fa la media delle previsioni di ciascun modello, spesso tagliando (drop, di fatto “ignorando” in maniera randomica) un certo numero di output di un layer, con il risultato di rendere il modello più robusto. Valori di dropout rivelatisi efficaci in questo esempio sono di 0,5/0,6.
Infine, è sempre opportuno usare l’equalizzazione con istogrammi (Local Istogram equalization) per migliorare le immagini con basso contrasto (come spesso sono le immagini del mondo reale).
Modello in Tensorflow
È arrivato il momento di implementare il modello di Deep Learning per classificare le immagini nel dataset. La matrice di convoluzione riconosce pattern direttamente dai pixel delle immagini con minima pre-elaborazione, “imparando” gerarchie di invarianti dai dati, ad ogni livello.
Usiamo a questo scopo Tensorflow, una libreria open source per l’apprendimento automatico con modelli già ottimizzati per questo compito. La nostra rete aggiornerà i “pesi” con un tasso di apprendimento di 0,001 per raggiungere un’accuratezza del 93% sul set di validazione.
Abbiamo citato in precedenza l’ottimizzazione di Adam (che è un acronimo per “ADAptive Moment Estimation,” algoritmo sviluppato nel 2015), grazie alla quale miglioriamo il training. Usiamo anche opportuni parametri di drop out e iniziamo ad addestrare il modello nella pipeline di training misurando, ogni volta la probabilità d’errore del modello. Sono necessarie varie iterazioni per addestrare il nostro modello. Abbiamo scelto deliberatamente di non mostrare codice ma questo è l’output che restituisce una semplice iterazione in Tensorflow con Keras:

Fonte: https://www.tensorflow.org/guide/keras/train_and_evaluate
Per quanto riguarda le API Keras, ci basterà usare Tensorflow, importare Keras e quindi i layer di Keras.
Epoch è semplicemente un periodo di tempo, identificato da un dato punto di inizio. Se definisco epoch come la mezzanotte del 1 gennaio 1970, per rappresentare il 2 gennaio 1970 basta fare: 60*60*24 e ottengo 86400. Prima di ogni epoch, il training set viene rimescolato. Al termine di ogni epoch, solitamente si misura la perdita e l’accuratezza sui set di training e di validazione
Dopo il training il modello viene salvato. Si passa all’esecuzione sul set di test, per capire se abbiamo sviluppato un modello sufficientemente buono. Se l’accuratezza è bassa già sul set di training, occorre calibrare i parametri (di shuffling, grayscale, normalization, istogram equalization), se invece l’accuratezza è buona sul set di training ma bassa su quello di validazione, è necessario agire sul dropout (overfitting).
Riportiamo per completezza l’iterazione del nostro modello su 20 epoch, per quanto riguarda il segnale di limite di velocità:
EPOCH 1 : Validation Accuracy = 82,453%
EPOCH 2 : Validation Accuracy = 86,765%
EPOCH 3 : Validation Accuracy = 90,213%
EPOCH 4 : Validation Accuracy = 91,520%
EPOCH 5 : Validation Accuracy = 90,668%
EPOCH 6 : Validation Accuracy = 92,608%
EPOCH 7 : Validation Accuracy = 92,902%
EPOCH 8 : Validation Accuracy = 92,585%
EPOCH 9 : Validation Accuracy = 92,993%
EPOCH 10 : Validation Accuracy = 92,766%
EPOCH 11 : Validation Accuracy = 93,356%
EPOCH 12 : Validation Accuracy = 93,470%
EPOCH 13 : Validation Accuracy = 93,832%
EPOCH 14 : Validation Accuracy = 94,603%
EPOCH 15 : Validation Accuracy = 93,333%
EPOCH 16 : Validation Accuracy = 93,787%
EPOCH 17 : Validation Accuracy = 94,273%
EPOCH 18 : Validation Accuracy = 92,857%
EPOCH 19 : Validation Accuracy = 93,832%
EPOCH 20 : Validation Accuracy = 93,605%
Sui segnali triangolari (pericolo), il modello non ha dato risultati altrettanto buoni. Non necessariamente per colpa del modello, ma a volte anche a causa della qualità delle immagini della specifica classe di segnale. Cartelli elaborati con scritte e simboli, danno risultati sicuramente più scadenti con probabilità di errore più alta.
Per chi vuole approfondire
Un buon dataset pubblico utile per mettere in pratica quanto esposto è reperibile qui: http://www.vicos.si/Downloads/DFGTSD (contiene più di 13.000 immagini e 200 diverse categorie di segnali stradali). In questo esempio, abbiamo usato Python come linguaggio di programmazione. Fra le funzioni e le librerie usate: skimage, matplotlib, scipy, oppure la distribuzione python Anaconda (che le contiene tutte ed è multipiattaforma) e TensorFlow per la classificazione delle immagini e la detection degli oggetti. Ci sono molti esempi online basati su TensorFlow 1.0. Qui abbiamo utilizzato TensorFlow 2.0 (con Keras) per classificare i segnali stradali.
Breve bibliografia:
Y. Zhu, C. Zhang, D. Zhou, X. Wang, X. Bai, and W. Liu, “Traffic sign detection and recognition using fully convolutional network guided proposals,” Neurocomputing, vol. 214, pp. 758–766, 2016.
D. Ciresan, U. Meier, J. Masci, and J. Schmidhuber, “Multi-column deep neural network for traffic sign classification,” Neural Networks, vol. 32, pp. 333–338, 2012.
P. Sermanet and Y. LeCun, “Traffic sign recognition with multi-scale Convolutional Networks,” in IJCNN, 2011, pp. 2809–2813.
La Guida Essenziale a ChatGPT per il 2025






